外观
推导
约 3306 字大约 11 分钟
2025-01-24
追本溯源
实际场景提出需求
假设有一组可以提出提案的进程集合,那么一致性算法需要保证一下几点:
- 这些提案只有一个被选中
- 如果没有提案被提出,那么不会有被选中的提案
- 当一个提案被选中后,进程可以获取被选中的提案信息
场景
以上是一个一致性算法,从实际场景触发得出的结论
精炼需求,得出安全性保障
对于一致性来说,安全性需求如下:
- 只有被提出的提案才能被选定
- 只有一个值被选定
- 如果某个进程认为某个提案被选定了,那么这个提案必须是真的被选中的那个
安全性
以上是一个一致性算法,从安全性得出的结论 安全性是一致性算法必须保障的
活性论点,优化算法
另一个一致性算法需要保证活性,所谓活性就是能正常的在一定时间内商定完成,确认一个被选中的提案
活性
活性不是必备的,但运用到实际生产中是必须的
推导约定与抽象
结合Paxos算法的背景故事,我们抽象出三类角色。
- Proposer 提案发起者
- Accpetor 提案授权者
- Learner 提案学习者[1]
推导过程
推导核心
在整个推到过程中,不应当按已经知道算法逻辑去推过程的想法进行。
应该这样去理解,即:
- 有目标,无过程。
- 前提条件可以大胆提出,有冲突的条件也可大胆提出,一步步去解决冲突,达到提出无冲突,可实现的前提条件。
- 摸着石头过河,最终能过河,就是推导出了一个一致性算法。
- 以下的P,皆为提出的前提条件。
注
假设不考虑信息被篡改的问题,信息被篡改不是一致性算法应该解决的问题。 Accpetor
提出P1
在只有一个提案被提出的情况下,依然可以选出一个提案,暗示如下:
- P1: 一个Acceptor必须批准它收到的第一个提案
在P1条件下,可以举例如下场景,进而对P1进行延伸
- 每个Acceptor接收一个提案导致平票
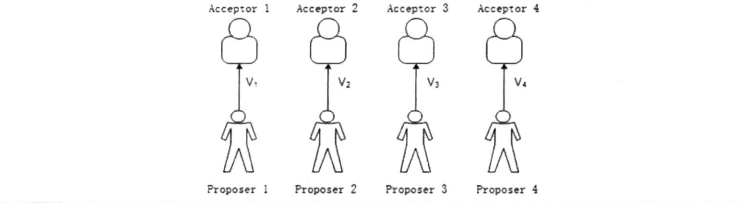
- Acceptor5因为短线,导致平票
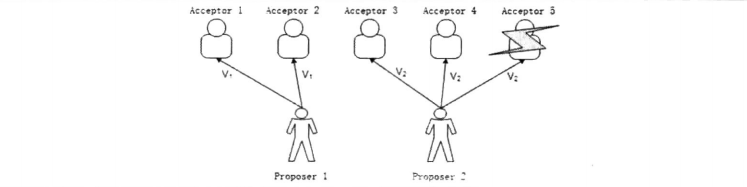
提出P2
由P1的场景1、2可以得出,单值V已经无法满足投票场景,因为在平票之后需要继续进行投票。
假设:
- 我们假定如果要选定一个提案,必须得到半数以上的批准。 被半数以上Acceptor批准的确认为选定。
- 由上述假设1得出,如果可能平票,则一个Acceptor必定不能只批准一个提案。 (若允许多次批准,该处暗含可能存在多个提案得到了多数Acceptor的批准,即多个提案得到的批准。)
我们继续假定能获取一个全局唯一的编号,结合V合成[编号,V]作为一个提案。
注
该处假设可能跨度较大,如果了解过Paxos算法的不要先入为主的带入Paxos的两阶段,当做第二阶段即可。
且并不是满足了假设2就完成了算法,应当把这个假设当成我们达成目标的一个先决条件。
在对P1结合实际情况推导并作出假设之后,可以得出P2。
P2: 如果编号为M0,Value为V0的提案被选定了,那么所有比编号M0更高的,且被选定的提案,其Value值必须也是V0。
注
由P2保证了上述假设2中暗含的,多个提案得到批准导致的选定了不同的value。
推导提示
在推导过程中,我们可以这样变通的去满足我们的条件。 即使用满足P2的另一个假设来替代P2。
进一步的,我们使用P2a代替P2。
P2a: 如果编号为M0,值为V0的提案被选定了,那么所有编号比M0高的,且被Acceptor批准的提案,值为V0。
此时根据下图的一个场景,Proposer2提出M0,V0,在全局序号的下一个提案M1,[M1,V1]被Proposer1提出, Proposer1在提出该提案时,由于Proposer2提出的[M0,V0]并未被选定,因此可以提出一个不同的Value值V1。 此时根据P1条件得出,Acceptor1必须批准[M1,V1],但是在批准前出现了多数批准了[M0,V0],与P2a矛盾。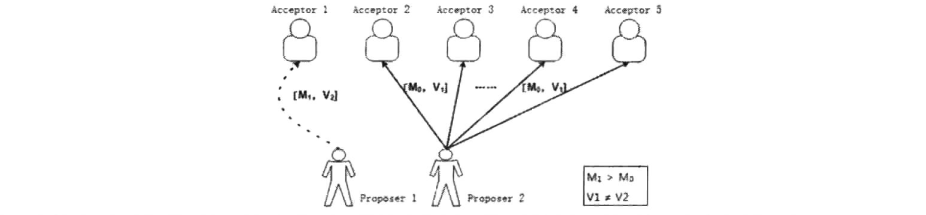
注
此处拆解一种场景,该种场景并不违反P1,P2a。 Proposer2的提案被Acceptor2,3批准,尚未被4或5批准。
Proposer1的提案被Acceptor1批准。 此时Proposer2的提案[M0,V0]尚未被选定(即大多数批准),因此Acceptor1批准[M1,V1]并不违反V1不为V0。
因此此时需要对P2a进行进一步的改造得到P2b,以解决与P1的冲突。 P2b: 如果编号为M0,值为V0的提案被选定了,那么所有Proposer产生的更高编号的提案,value值必须为V0。
注
此处的解决手段为,进一步从源头限制[M1, V1]的产生,从而不会出现批准不同值V1的情况,即满足P1,修改P2a。
注
P2b实际上并不是完美包含P2a,因为P2b中Proposer1可能在Proposer2的[M0,V0]选定之前产生了提案[M1,V1],
并不违背P2b,但是Acceptor1在接受到该提案[M1,V1]之前,Proposer2的[M0,V0]由于被多数选中而被选定。 此后Acceptor1再被Proposer1按照P1要求被批准。
P2b强调了,[M0,V0]被选定,之后产生的提案才需限定Value微V0。
相当于对P2a中,[M0,V0]被选定之前的提案并未做出限制。此处之后再议。
为了方便P2b的实现,进一步提出P2c。 P2c:对于任意的Mn和Vn,如果[Mn,Vn]被提出,那么肯定存在一个半数以上的Acceptor组成的集合S,满足以下两个条件的任意一个:
- S中不存在任何批准过编号小于Mn的提案的Acceptor。
- 选取S中所有Acceptor批准的编号小于Mn的提案,其中编号最大的那个提案的Value值是Vn。
注
此处可能难以理解P2c究竟如何利于工程化的实现。 实际上Proposer提出某个提案[Mn,Vn]之前,会先去向一个半数以上的Acceptor组成的集合S确认,若均为批准提案。 则适用于P2c的情况1,可以按自己需要随意提出value值。
若存在被批准的提案(此处指的是批准,不是选定),则找比当前Mn小的最到的Mx的值Value作为Vn提出。
注
对P2c的情况2的进一步理解。
Proposer1,2,3,4某一时刻同时提出一堆提案,由于是并发的,所以可以同时进入情况1,并且提出不同的值,如:
[M1,V1],[M2,V2],[M3,V3],[M4,v4](前看P2b,此处不违反P2b,因为产生提案的时刻并不存在被选中的提案)
某个时刻[M3,V3]得到了多数批准,如Acceptor1,2,3。假设之后Proposer5再次产生一个新的提案, Proposer5向任意一个半数集合S发起查看批准提案的请求(例如1,2,3或者3,4,5必定包含了[M3,V3]), 按P2c的情况2感知到[M3,V3],则发起[M5,V3]。
可能有人会疑惑如果Accepter1,2,3接收了[M3,V3],Acceptor4,5接收了[M4,V4],那么[M5]的值有可能取到V4。
所以此处隐含了一个问题我们必须要保证并发的提出M3,M4的时候,不可能让V4的值与被选定的V3不同。 值得思考的是,我们要么保证如果提出了[M4,V4]那么必定不能让[M3,V3]被选定,要么保证[M3,V3]被选定之后,[M4,V4]的V4值即为V3。 实际上上述跳过了[M4,V4],值得一提的是我们必须保证V4与V3相同。
针对上述P2c提出的问题,我们需要采用两阶段提交来保证。
阶段一:
- Proposer选择一个提案编号Mn,然后向Acceptor的超过半数的子集成员发生编号Mn的Prepare请求。
- 如果一个Acceptor接收到编号Mn的Prepare请求吗,且编号Mn大于该Acceptor已经响应的所有Prepare请求的编号, 那么它就会将它已经批准过的最大编号的提案作为响应反馈给Proposer,同时该Acceptor会承诺不会批准任何小于Mn的提案。
阶段二:
- 若果Proposer收到来自半数以上的Acceptor对于其发出的编号为Mn的Prepare请求的响应,那么它就会发送一个针对 [Mn,Vn]的提案的Accept请求给Acceptor。Vn即为收到的响应中的编号最大的提案的值,如果响应中不包含值,那么它就是任意值。
- 若果Acceptor收到这个针对[Mn,Vn]提案的Accept请求,只要该Acceptor对编号大于Mn的Prepare请求做出响应, 它就可以通过这个提案。
两阶段提交解决了P2c的问题,P2c通过向大多数获取最接近提案编号Mn的值满足了P2b对proposer生成提案value的要求。
P2b通过更严格的生成标准,从Proposer生成提案的角度确保了满足P2a的Acceptor批准要求。
P2a通过更严格的批准标准,从Acceptor批准提案的角度满足了P2对提案选定值Value的一致要求。
P2c >= P2b >= P2a >= P2
由于两阶段提交的要求,对P1产生新的推导,产生P1a。 P1a: 一个Acceptor只要尚未响应过任何编号大于Mn的Prepare请求,那么它就可以接收这个编号为Mn的提案。
P1a >= P1
因此使用两阶段提交的步骤,可以满足P1a和P2c,且不会产生冲突。
最终实际满足P1和P2来达到一致性的要求。
Deepseek总结
以下通过Deekseek的解释,精简的总结Paxos协议。
协议内容
Paxos算法中的P1、P2、P2a、P2b、P2c是Leslie Lamport在论文中提出的关键约束条件,用于确保分布式系统在异步网络中达成一致。以下是它们的定义和演进逻辑:
P1(基础约束) 定义:一个Acceptor必须接受它收到的第一个提案。 问题:如果多个Proposer同时发起不同提案,可能导致无法达成一致(活锁)。因此需要后续条件修正。
P2(核心一致性) 定义:若某个提案[n, v]被选定(即被多数派接受),则所有更高编号的提案选定的值必须也是v。 目标:保证一旦某个值被选定,后续所有提案必须沿用该值。
P2a(Acceptor视角的强化) 定义:如果提案[n, v]被选定,则任何Acceptor接受的更高编号提案的值必须是v。 问题:Acceptor可能无法及时感知已选定的提案(例如网络延迟),导致无法满足条件。
P2b(Proposer视角的强化) 定义:若提案[n, v]被选定,则之后所有Proposer提出的更高编号提案必须使用v。 实现方式:Proposer在提出新提案前,需通过准备阶段(Prepare Phase)获取已接受的最大编号提案的值v,并承诺后续提案沿用v。
P2c(最终约束) 定义:Proposer在提出提案[n, v]前,必须确认以下两者之一:
- 存在多数派Acceptor已接受的提案中,最大编号提案的值为v;
- 若没有已接受的提案,则v可自由选择。 关键:通过两阶段提交(Prepare + Accept)确保新提案与历史多数派一致。
演进逻辑
P1尝试直接约束Acceptor,但存在活锁问题。
P2提出核心一致性目标,但未明确实现方式。
P2a/P2b试图从Acceptor或Proposer视角强化约束,但存在可行性问题。
P2c通过两阶段提交机制(准备阶段收集信息 + 接受阶段提交提案)最终满足P2b,从而保证一致性。
总结
Paxos通过逐步细化约束条件,最终以P2c为核心,结合两阶段提交和多数派原则,解决了分布式环境下的一致性问题。其核心思想是:
准备阶段:Proposer通过多数派获取历史最高提案值,避免冲突。
接受阶段:基于准备阶段的信息提交新提案,确保与已选定值一致。 这些约束共同保证了算法的安全性(Safety)和活性(Liveness)。
实际场景中用于学习一个被选定提案的角色 ↩︎
